对ABFT容错的浅薄理解
原理是针对某一种算法中的高频算子进行可靠性设计,以在较低的成本下保障算法大部分的可靠性。目前看到的两篇论文都是通过冗余计算,计算校验和对比结果来实现容错机制。这种方法相比于架构层和电路层的方法来说代价要更低,更加灵活。
相关论文的主要方法是:
设计校对矩阵
设计checksum校对方法
分析一下校对算法开销如何、能够实现什么级别的容错(可检测or可修正)
设计相关的容错框架或者系统
通过实验验证可靠性保证以及额外开销。
以后也可以多思考一下相关的算子有没有这样的机会做冗余计算。
矩阵操作ABFT设计
原文:Algorithm-Based Fault Tolerance for Matrix Operations(1984, TC)
校对矩阵设计
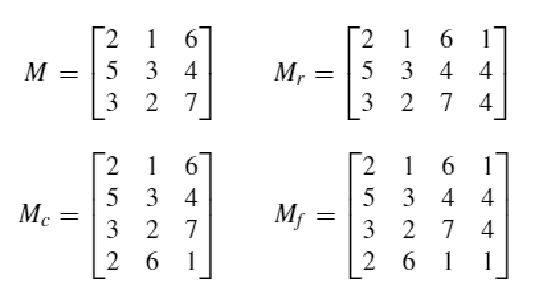
简单来说就是有个矩阵M,然后里面每个元素的最大值(位宽决定)为8。这个矩阵的行校验矩阵$M_r$就是增加新的一列,这一列是前面几列的和,这个矩阵可以用来定位错误所在的行;同样这个矩阵的列校验矩阵$M_c$也同理定义,用来定位错误所在的列。$M_f$是矩阵的全校验矩阵,可以实现错误的定位和修复。
检错方法
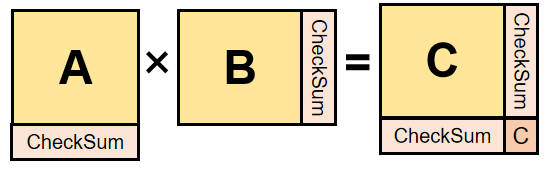
- 适用于矩阵乘、加、LU分解、标量乘、转置操作
- 可以实现单比特错误检测(右下角的数值C和整个结果矩阵的和对比)、定位、纠错(通过行和列定位后再算一下)
- 可以实现多比特错误检测。
卷积操作ABFT设计
FT-CNN: Algorithm-Based Fault Tolerance for Convolutional Neural Networks
校对矩阵
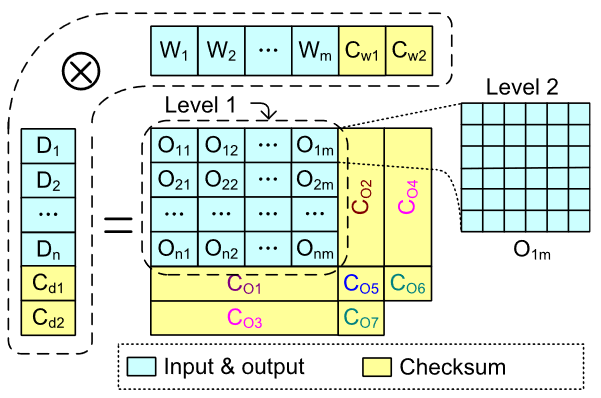
在这个卷积操作里面假设输入矩阵D和W都是思维矩阵,校对矩阵中$C_{d1}$和$C_{d2}$分别是$D_i$的和以及加权和。如果在全校验的情况下,checkSum会有很多个;不同的checkSum的计算难度不同,其检错难度也不同,因此适用于不同的场景,或者可以分层次进行检测,以使本方法的开销更小一些。这就是本文的核心思想,其具体思路可以再重新找一下论文。
不同校验和组合产生的检错维度

检测原理:以Checksum of Checksum为例
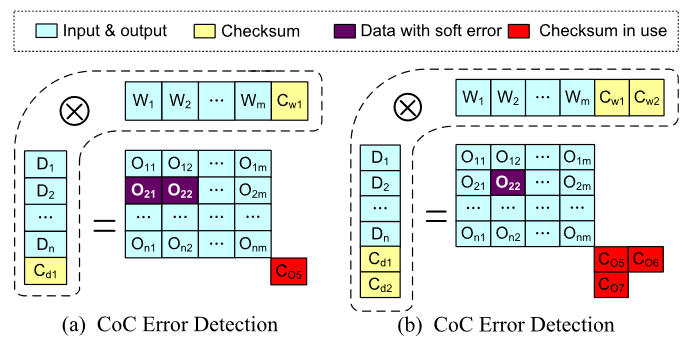
检错能力和checksum的复杂度分析

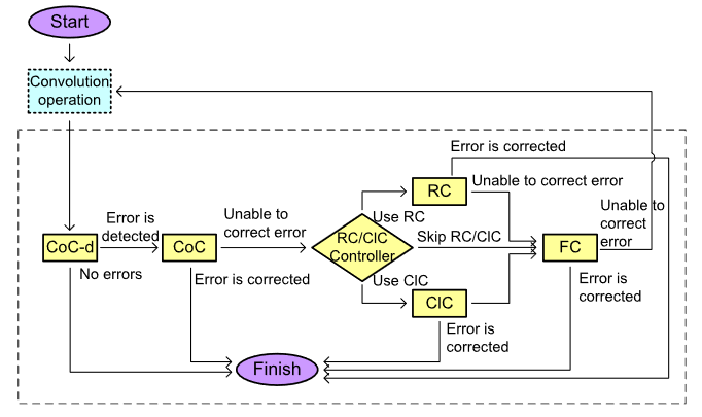
分层的纠错框架
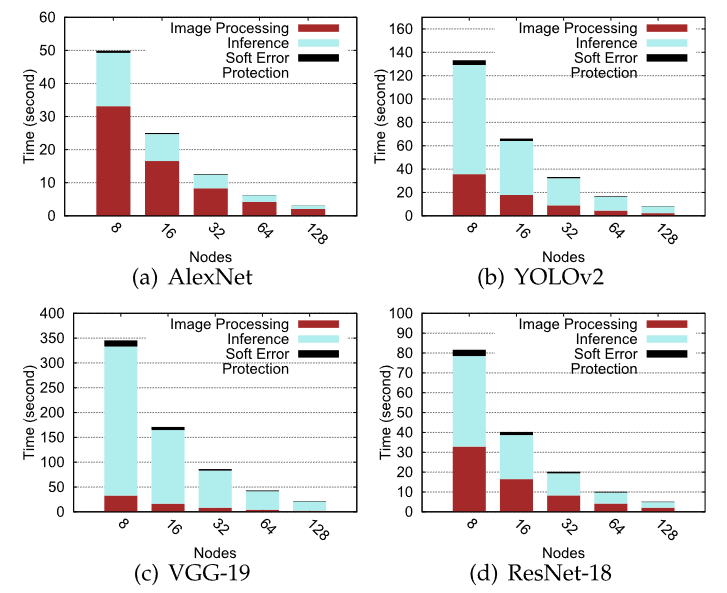
实验结果:开销
- 本文作者: Zhang Xinmiao
- 本文链接: https://recoderchris.github.io/2023/02/08/ABFT/
- 版权声明: 本博客所有文章除特别声明外,均采用 MIT 许可协议。转载请注明出处!


